Abstract: This paper presents a theoretical model, which I believe to be novel, for designing neural nets. This model has several interesting characteristics: it is local (that is, no "global goal" is required for learning); it is modeless (there is no separate "learning phase"); and it is imaginative (it should have a "mind's eye", which we could usefully observe). Along with the model are presented supporting observations from human cognition, which inspired it.
This paper explores a possible model for building Artificial Neural Networks, one which appears to differ in several important respects from any existing models I know of. The ensuing is a bit wordy by the standards of most papers; my apologies for this, but I suspect that one can not really understand the logic behind the model without exploring the problems it attempts to remedy. (This is particularly important, as the model is currently untested -- if there are failings in the details, I hope that others can follow the same chains of logic and come up with more robust solutions.)
To begin with, we should look at a few of the problems with most models of Artificial Neural Networks, when compared with natural cognition:
First, they have a tendency to be highly modal. That is, they draw a clear distinction between a "learning mode", wherein you train the network to recognize particular data and classes, and a "play mode", wherein you feed inputs to the network, and get outputs from it. Rote school learning aside, this doesn't seem to match natural learning at all -- we learn as we act, continuously. (Indeed, even in schools, "learning by doing" is increasingly seen as an effective paradigm.)
Second, they tend to learn in a very global manner. The inputs and outputs of the network tend to be large objects, spanning significant numbers of neurons, and training must therefore be controlled from the top. (For example, the standard reweighting mechanisms which examine the prospective output, then adjust one or more neurons based on that end result.) Even in most "self-organizing" models, the training is still global in this sense, with some global process setting the neurons. This seems biologically implausible, although not impossible -- it would make much more sense if each neuron was largely self-contained, and "learned" for itself. If nothing else, this seems necessary in order to account for the speed at which we learn, considering the snail's pace of bioneural processing.
Third, almost all models have a strong differentiation between input and output. That seems sensible from a biological viewpoint (since we clearly have "input" and "output" organs). But is it? Very little that we do is simple unidimensional i/o. Rather, we are powerful processors of associations, taking a wide variety of sensory input, combining it, and associating it with a large mental "database" ranging from the highly concrete to the extremely abstract. Even when we do perform "i/o", it tends to be extremely complex and multidimensional. (Contemplate for a moment all the forms of input and output involved in typing this essay on the computer.)
Keep these issues in mind; they form much of the motivation for this idea.
Consider for a moment how you think and learn. You go through your day, performing countless actions on a routine basis, and getting all kinds of sensory input. The sound of the alarm clock, the smell of morning coffee, the feel of the air as you step into winter cold. All are inputs, but none teach you anything -- they are experienced, noted briefly, and then lost as you go on to other things. If you are typical, you won't be able to recall any of them clearly in a fairly short period of time. (Unless you are concentrating on remembering them, which is in itself unusual.)
You learn only from the experiences which are novel. The sound of a fire alarm and the smell of burnt toast teach you to turn down the toaster. These experiences are not normal to your daily routine, so you do notice them, do remember them, and do learn from them.
This is important, and too often overlooked. We only learn from novelty. The more routine something is, the less likely we are to actually learn from it. Even discomforts and pains, when routine, will cease to teach.
So what is novelty? It is the violation of expectations. At any given point, you are expecting a vast number of things. You expect there to be air to breathe. You expect the predominant smell in the air to be coffee. You expect to find butter in the refrigerator for that toast. You aren't consciously aware of most of these expections, but they are always there, and become quickly noticed when things go wrong. Consider how natural it is to say, "That isn't right", even when you can't put your finger on precisely what "that" is.
Carry this further, and consider the degree to which our expectations work -- consider the "mind's eye". We are quite capable of imagining sensations of every sense. Pause, for a moment, and envision the face of someone you know well. Hear a catchy tune you've heard too often on the radio (don't hum it -- just hear it). Imagine the sensation of velvet under your fingers. All of these sensations are a bit indistinct and low-resolution, but all are easy to feel. Why? I posit that this mechanism is part and parcel with the concept of "expectations"; it is indicative of the heavy feedback loops present in the human brain, which are there specifically to permit expectation -- which, as we have just examined, is the key to human learning.
From this follows the model below -- a model of neural networks designed to have strong expectations, and to learn directly from violations of them.
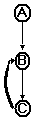
Take a trivial network, whose structure looks like this. A, B, and C are each layers of neurons; the exact number of neurons within each layer is irrelevant. The layers are connected along the arrows; that is, layer A has a substantial connection to B, B to C, and C has a thick feedback layer to B (possibly thicker than the connection from B to C).
Layer A represents the raw input from the "senses", corresponding to something like the retina, or the ciliae in the ear. This has a close and constant connection to layer B, maybe a 1-to-1 connection. B represents the "concrete processing" of the input. This is then fed to layer C, the "abstract processing" of the input (which corresponds roughly to the "hidden layer" in most conventional models).
So far, this is much like a normal feedback network. What makes it unusual is in how the neurons are "trained". In conventional models, C would lead to an "output". We would set layer A to an input, then compare the output from C with our desired output, adjust the neural weights fractionally, and try again. In this model, however, the neurons are acting individually, and are each seeking stability.
Think back to the earlier discussion of expectations, and their role in learning. The purpose of the thick feedback loop from C to B is to present B, at any given time, with C's expected input. This is then melded in some fashion (I am, for the moment, not dealing with the exact neural activation function) with the actual input. If the result matches C's expectations, the network is more-or-less stable. If, on the other hand, the results are novel, the network is destabilized, and the neurons in C begin to fluctuate, since the feedback and the input are mismatching.
Each neuron detects this instability on its own; neurons whose state is remaining relatively stable will not be affected. The exact function for detecting instability deserves further research -- it probably should require a number of cycles of fluctuation before deciding that it is unstable, and probably should be designed to permit gradual changes in activation levels smoothly. We should, therefore, perhaps refer to the desired neural state as "quasi-stability" -- changing, but only to mild degrees.
When a neuron detects that it is unstable, it begins reweighting its inputs. Again, the exact mechanism deserves more research, but one possibility, based on synaptic resistance, is presented in the next section. Eventually, the theory runs, the network will again settle down to a quasi-stable state, with the feedback loop and the inputs matching reasonably well. The network has now adjusted a bit, to cope with this particular new input.
Of course, as presented this model doesn't match cognitive reality very well -- no real brain is nearly this simple. To make this more realistic, if more complicated, add a layer D below C. D represents higher cognitive functions, such as planning and abstract thought. D should have a thick feedback loop into C, just as C has to B. Thus, when novel input arrives, C has feedback from D, acting as a sort of stabilizing brake on the confusion coming in from B. This may account for why biological networks tend to have such thick feedback networks: we need that strong feedback of expectation, to prevent novel inputs from causing complete network chaos. We have a strong bias towards fitting the new input into the framework of preconception that already exists.
More details and ideas are discussed below, but this is the essence of what I will call (risking humiliation) the Waks Neural Model: a network with extremely strong feedback at all levels, where neural weighting is conducted by each neuron individually, and where each neuron is seeking quasi-stability.
The next step, obviously, is to start filling in some of the gaping holes of vagueness in the above description. The first step is to consider how the neuron reweights itself, which begs the question of what a neural weight is.
For the moment, I am going to ignore the question of whether the neural activation function is linear or not. In most traditional ANN models, the function is non-linear -- once a neuron's inputs reach a critical threshold, the neuron "fires" at a level not proportional to those inputs. The alternative is a linear model, where the "level" of the neuron is proportional to the sum of its inputs. I think both should be examined.
Regardless, it is clear what some of the needs of this model are. We need some mechanism for measuring neural weight which can be adjusted locally -- the neuron and the synapses leading into or out of it must contain enough information to do the reweighting by itself.
(Jargon warning: a "synapse", for purposes of this discussion, is really just a connection between two neurons. I am primarily dealing with incoming synapses here, the ones that tell the neuron what to do.)
The simplest idea would be to simply adjust synaptic weight, based on the stability of the synapses. Since the neuron's weight is in some fashion related to its inputs (regardless of whether the function is linear or not), it is clear that the neuron's stability is related to the stability of the synapses. So, give each synapse enough "memory" to track its stability, in much the same way we do the neuron itself. Each synapse also has a "resistance"; the higher the resistance, the less activation the neuron will get from that synapse. Go through the synapses in parallel, increasing the resistance of unstable synapses, and lowering that of stable ones. This should be done in small increments, but should probably be re-examined every cycle.
That version is a little naive; while it might work, I worry that it could tend towards a minimalist solution, with a high resistance on all synapses, and little input coming through. If this proves to be the case, an alternative could be tried, wherein the neuron has a finite "quantity" of resistance. During adjustment, this resistance is reallocated from the stabler synapses to the more unstable ones. This version would be less likely to "deaden", but might be harder to stabilize. Both should probably be tried.
Another variation in the model concerns when to reweight. As described above, "novelty" is a non-linear function -- when the instability reaches a particular point, the neuron starts reweighting. Alternatively, novelty could be linear: the neuron is always reweighting, but the degree of reweighting is proportional to the instability of the neuron. Intuitively, I think this variant may be a bit more plausible, and possibly easier to program. (But more cycle-consuming, since you are performing slight tweaks on every neuron (and maybe every synapse) every cycle.)
As described, the Waks Neural Model is interesting, but essentially a curiosity. The traditional neural model, with distinct inputs and outputs, may be a bit artificial, but it it useful; it makes a nice pattern-matching engine. Are there uses for this model?
One characteristic of this model, distinct from most neural models, is that it is unusually scaleable. Since the neurons are distinct and independent, it is highly amenable to massively parallel processing; indeed, it is well-suited to simple SIMM machines. Also, since there is no concept of global "goals", it is well-suited to arbitrarily structured, complex neural arrangements. It should be able to model brain functions more easily than most neural networks.
In the long run, a realistic brain model means that we should be able to figure out how to "teach" a network, much as one teaches real brains, and get useful output from it. This promises to be very complex, though -- we aren't especially good at teaching humans, so it isn't clear that we will be efficient at teaching ANNs.
In the shorter run, though, there may be a good way to use these networks: we can tap "the mind's eye" of this machine.
Consider the diagram suggested earlier, with at least four layers of neurons, the top layer (D) being higher cognitive function. Now, connect several of these networks at this top layer, each one connected into a richly interconnected hidden layer at the top, so that the "senses" all share the same cognitive layer. In theory, this network should be mildly sensitive to correlations between the "senses"; in short, it should be an associative memory.
Now, remember the discussion of the "mind's eye" earlier. This is one of the major inspirations for this model -- each layer is passing strong feedback to the more primitive layers above it. We should be able to examine that feedback by shutting off the direct inputs (layer A), and reading in the contents of layer B. If the connections between A and B are straightforward, the feedback weights from C to B should bias towards similarly straightforward interpretation. B should be serving as the mind's eye, and we should be able to examine that. To be sure, the results will probably be low-resolution. A high-resolution mind's eye would be marvelously useful, but even at low-res we can probably make considerable use of it.
Combine this mind's eye with the multi-sense associative design, and it starts becoming truly useful. Data is presented to the network in many senses at once; our definition of "sense" can be whatever is useful to the application. Queries into this "database" are simple: present the fields of data we do know to the appropriate senses, and read out the expectations on the mind's eye of the sense we are curious about. In theory, it should even have the usual neural-net characteristic of making intelligent guesses about novel data, presenting sensible expectations for that data.
The above is really just a start, a rough architecture that still needs to be fleshed out into a design. A number of areas need to be explored, including:
And so on. I don't have the time to perform these experiments myself; my professional obligations keep me from spending much time on this. I would love to talk with anyone interested in implementing these ideas and playing with them. (Any students looking for a good term project?)
The above is a collection of theories and ideas, unfortunately lacking much empirical underpinning. I have written it up because the ideas seemed to be new, and I thought they should be shared. I welcome any and all correspondence on the subject, whether it be to tell me that I've reinvented a wheel that was rejected a decade ago, or that this really is something new and different. I think the field of neural networks is ready to progress onto more realistic and interesting nets; I hope that this model is a useful step towards that.
And please, if you've found this interesting, pass on the URL...
A number of disclaimers seem warranted, so that this paper is interpreted correctly.
First, I should reiterate: everything here is hypothesis. I am attempting to write up gut instincts, rather than working code. I would love to see these ideas implemented (and again, I would like to talk to anyone who wants to try), but I simply don't have the time myself. Hypothesizing is cheap (I mostly do it in bed between 2 and 5 in the morning), but coding time is precious.
Second, there are a bunch of unproven guesses in here. I would guess that the biggest one is that independent neurons will live together in something resembling harmony, but that's far from the only questionable assumption. Don't get too wedded to any of the details; the ideas behind them are considerably more important.
Third, I am not exactly a specialist in this field. I have been interested in synthetic cognition for over a decade, and have quietly paid attention to the broad sweep of ideas, but I am primarily a software architect. Consider me an enthusiastic amateur with a bit of insight. (And no, I don't have a Ph.D. in anything.)
Fourth, since I am not an expert here, it is possible that I am reinventing the wheel. I have attempted to skim through the literature, and haven't found anything terribly close to these theories, but it's entirely possible that I have overlooked something. It's certainly related to the Hopfield network, but appears to differ in several key respects. Sorry if I step on any toes (and if I havereinvented the wheel, I would appreciate pointers to the previous citations).
Finally, once again, my apologies if any of this is excessively wordy or unclear. I am breaking enough of the usual rules of neural network design that it is difficult to keep to the usual concise jargon. Please write to me if you have any questions or comments on the paper.
Mark Waks